Algorithms

Algorithm Analysis

In computer science, the analysis of algorithms is the determination of the amount of resources (such as time and storage) necessary to execute them.

Overview

Usually, the efficiency or running time of an algorithm is stated as a function relating the input length to the number of steps (time complexity) or storage locations (space complexity). Algorithm analysis is an important part of a broader computational complexity theory, which provides theoretical estimates for the resources needed by any algorithm which solves a given computational problem. These estimates provide an insight into reasonable directions of search for efficient algorithms. In theoretical analysis of algorithms it is common to estimate their complexity in the asymptotic sense, i.e., to estimate the complexity function for arbitrarily large input. Big O notation, Big-omega notation and Big-theta notation are used to this end.

  • Rule of thumb: Simple programs can be analyzed by counting the nested loops of the program. A single loop over n items yields f( n ) = n. A loop within a loop yields f( n ) = n2. A loop within a loop within a loop yields f( n ) = n3.
  • Rule of thumb:Given a series of for loops that are sequential, the slowest of them determines the asymptotic behavior of the program. Two nested loops followed by a single loop is asymptotically the same as the nested loops alone, because the nested loops dominate the simple loop.
Asymptotic comparison operator Numeric comparison operator
Our algorithm is o( something ) A number is < something
Our algorithm is O( something ) A number is ≤ something
Our algorithm is Θ( something ) A number is = something
Our algorithm is Ω( something ) A number is ≥ something
Our algorithm is ω( something ) A number is > something

Fig 1: This graph shows the different growth of functions, cubix: f(x^3), linear: f(x) etc.

Compute the Time Complexity Using Summations

randerson112358

Learn how to solve a programs time complexity, using summations.

Download PDF

Run-time analysis Orders of growth

Run-time analysis is a theoretical classification that estimates and anticipates the increase in running time (or run-time) of an algorithm as its input size (usually denoted as n) increases. Run-time efficiency is a topic of great interest in computer science: A program can take seconds, hours or even years to finish executing, depending on which algorithm it implements (see also performance analysis, which is the analysis of an algorithm's run-time in practice).

Name Complexity class Running time (T(n)) Examples of running times Example algorithms
constant time O(1) 10 Determining if an integer (represented in binary) is even or odd
inverse Ackermann time O(α(n)) Amortized time per operation using a disjoint set
iterated logarithmic time O(log* n) Distributed coloring of cycles
log-logarithmic O(log log n) Amortized time per operation using a bounded priority queue[2]
logarithmic time DLOGTIME O(log n) log n, log(n2) Binary search
polylogarithmic time poly(log n) (log n)2
fractional power O(nc) where 0 < c < 1 n1/2, n2/3 Searching in a kd-tree
linear time O(n) n Finding the smallest item in an unsorted array
"n log star n" time O(n log* n) Seidel's polygon triangulation algorithm.
linearithmic time O(n log n) n log n, log n! Fastest possible comparison sort
quadratic time O(n2) n2 Bubble sort; Insertion sort; Direct convolution
cubic time O(n3) n3 Naive multiplication of two n×n matrices. Calculating partial correlation.
polynomial time P 2O(log n) = poly(n) n, n log n, n10 Karmarkar's algorithm for linear programming; AKS primality test
quasi-polynomial time QP 2poly(log n) nlog log n, nlog n Best-known O(log2 n)-approximation algorithm for the directed Steiner tree problem.
sub-exponential time
(first definition)		 SUBEXP O(2nε) for all ε > 0 O(2log nlog log n) Assuming complexity theoretic conjectures, BPP is contained in SUBEXP.[3]
sub-exponential time
(second definition)		 2o(n) 2n1/3 Best-known algorithm for integer factorization and graph isomorphism
exponential time E 2O(n) 1.1n, 10n Solving the traveling salesman problem using dynamic programming
factorial time O(n!) n! Solving the traveling salesman problem via brute-force search
exponential time EXPTIME 2poly(n) 2n, 2n2
double exponential time 2-EXPTIME 22poly(n) 22n Deciding the truth of a given statement in Presburger arithmetic

Time complexity - Compute the time complexity of the following code

randerson112358

Compute the complexity of the following code fragment.

Download PDF

Analysis Types

The algorithm complexity can be best, average or worst case analysis. The algorithm analysis can be expressed using Big O notation. Best, worst, and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively. The big o notation simplifies the comparison of algorithms.

Best Case

Best case performance used in computer science to describe an algorithm’s behavior under optimal conditions. An example of best case performance would be trying to sort a list that is already sorted using some sorting algorithm. E.G. [1,2,3] --> [1,2,3]

Average Case

Average case performance measured using the average optimal conditions to solve the problem. For example a list that is neither best case nor, worst case order that you want to be sorted in a certain order. E.G. [2,1,5,3] --> [1,2,3,5] OR [ 2,1,5,3] --> [5,3,2,1]

Worst Case

Worst case performance used to analyze the algorithm's behavior under worst case input and least possible to solve the problem. It determines when the algorithm will perform worst for the given inputs. An example of the worst case performance would be a a list of names already sorted in ascending order that you want to sort in descending order. E.G. [Abby, Bill, Catherine] --> [Catherine, Bill, Abby].

Best, Worst, and Average case

randerson112358

Understand analysis types: Best, Worst, and Average case algorithm analysis.

Algorithms efficiency described in terms of Time and Space. The time efficiency calculated using CPU utilization. The Space efficiency calculated using memory and disk usage of an algorithm. The developer should know the difference between Performance and complexity. The complexity analysis does not depend on any computer resource. It may change based on the input size. The algorithm performance is machine independent and does not depend on any other factors.

Recursive Complexity

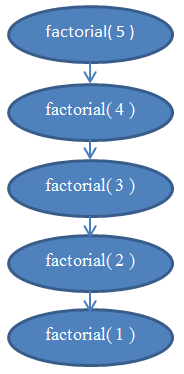
dionyziz

Let's now take a look at a recursive function. A recursive function is a function that calls itself. Can we analyze its complexity? The following function, written in Python, evaluates the factorial of a given number. The factorial of a positive integer number is found by multiplying it with all the previous positive integers together. For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1. We denote that "5!" and pronounce it "five factorial"

1.def factorial( n ):
2.    if n == 1:
3.        return 1
4.    return n * factorial( n - 1 )

Let us analyze the complexity of this function. This function doesn't have any loops in it, but its complexity isn't constant either. What we need to do to find out its complexity is again to go about counting instructions. Clearly, if we pass some n to this function, it will execute itself n times. If you're unsure about that, run it "by hand" now for n = 5 to validate that it actually works. For example, for n = 5, it will execute 5 times, as it will keep decreasing n by 1 in each call. We can see therefore that this function is then Θ( n ).

If you're unsure about this fact, remember that you can always find the exact complexity by counting instructions. If you wish, you can now try to count the actual instructions performed by this function to find a function f( n ) and see that it's indeed linear (recall that linear means Θ( n )).

See Figure 5 for a diagram to help you understand the recursions performed when factorial( 5 ) is called.This should clear up why this function is of linear complexity.

Solution :

factorial( 5 ) -> factorial( 4 ) -> factorial( 3 ) -> factorial( 2 ) -> factorial( 1 )

Solve Big Oh, Big Theta, and Big Omega Using Limits

Limit Asymptotic Theorem: lim( x -> inf) f( x ) / g( x ) = L
Source: Click Here
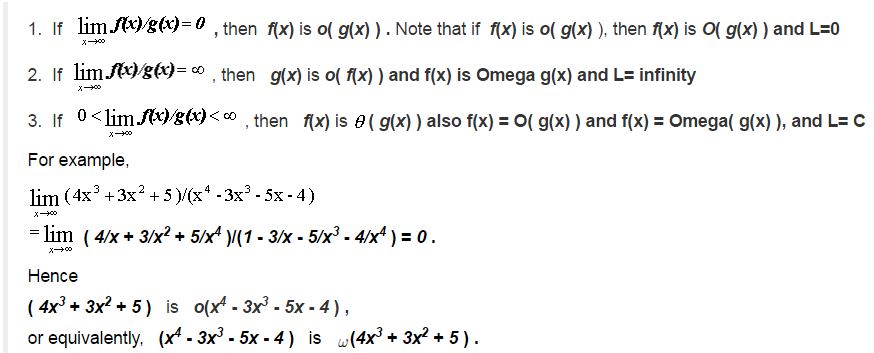
Asymptotic Limit

Solve Big Oh: Using Limits

This video shows a quick way to prove a function is Big-Oh, Big-Theta, or Big-Omega

Understanding Code Complexity

The algorithm complexity ignores the constant value in algorithm analysis and takes only the highest order. Suppose we had an algorithm that takes, 5n^3+n+4 time to calculate all the steps, then the algorithm analysis ignores all the lower order polynimials and constants and takes only O(n^3).

Simple Statement

This statement takes O(1) time.

int y= n + 25;

If Statement

The worst case O(n) if the if statement is in a loop that runs n times, best case O(1)

if( n> 100)
{
…
}else{
..
..
}

For / While Loops

The for loop takes n time to complete and and so it is O(n).

for(int i=0;i<n;i++)
{
..
..
}

The while loop takes n time as well to complete and so it is O(n).

int i=0;
while( i<n)
{
..
i++;
}

If the for loop takes n time and i increases or decreases by a constant, the cost is O(n)

for(int i = 0; i < n; i+=5)
   sum++;

for(int i = n; i > 0; i-=5)
   sum++;

If the for loop takes n time and i increases or decreases by a multiple, the cost is O(log(n))

for(int i = 1; i < =n; i*=2)
   sum++;

for(int i = n; i > 0; i/=2)
   sum++;

Nested loops

If the nested loops contain sizes n and m, the cost is O(nm)

for(int i=0;i<n;i++)
{
    for(int i=0;i<m;i++){
    ..
    ..
    }
}

If the first loop runs N times and the inner loop runs log(n) times or (vice versa), the cost is O(n*log(n))

for(int i=0;i<n;i++)
{
    for(int j=1;i<=n;j*=4){
    ..
    ..
    }
}

If the first loop runs n2 times and the inner loop runs n times or (vice versa), the cost is O(n3)

for(int j=0;j<n*n;j++)
{
    for(int i=0;i<n;i++){
    ..
    ..
    }
}

If the first loop runs n times and the inner second loop runs n2 times and the third loop runs n2, then O(n5)

for(int i = 0; i < n; i++)
    for( int j = 0; j < n * n; j++)
        for(int k = 0; k < j; k++)
            sum++;

Summation_Theta_Approx.jpg

Solve Big Oh: By definition

In this video learn how to easily prove f(n) = O(g(n) using only the definition of what it means for a function f(n) to be Big-Oh of another function g(n).

Algorithm Analysis IMG

Algorithm Analysis Tutorial

Code: Factorial Takes Θ(n) time

/*
 This program outputs the factorial of a number e.g. 5! = 5 * 4 * 3 * 2 * 1 = 120.
 In general n! = n * n-1 * n-2* ... * 3 * 2 * 1
 By: Rodney Anderson
 
 */

# include <stdio.h>

int fact_recursive(int n);// This is a recursive factorial function
int fact_iterative(int n);// This is a iterative factorial function

int main(void)
{
  int n;
  
  printf("Enter a number: ");
  scanf("%d", &n);
  
  printf("%d! = %d\n", n, fact_iterative(n));
  
  system("pause");
}

fact_recursive(int n)
{
  //Base Case
  if(n == 0)
  return 1;
  
  return n *fact_recursive(n-1);
}

int fact_iterative(int n)
{
  int i;
  int product = 1;
  for(i = 1; i<= n; i++)
  {
    product = product * i;
  }
  
  return product;
}

Copyright © 2013, Everything Computer Science.