Discrete Mathematics
Sets
A set is a collection of distinct objects.
Overview:
A set is a well defined collection of distinct objects. The objects that make up a set (also known as the elements or members of a set) can be anything: numbers, people, letters of the alphabet, other sets, and so on. Georg Cantor is the founder of set theory. Sets are conventionally denoted with capital letters. Sets A and B are equal if and only if they have precisely the same elements.
Basic Set Theory, Part 1
Mike BlackBasic Set Theory Part 1 - Introduction to Sets and Set Notation
Download PDFSpecial Sets Common Universal Sets
There are some sets that hold great mathematical importance and are referred to with such regularity that they have acquired special names and notational conventions to identify them. One of these is the empty set, denoted {} or ∅. Another is the unit set {x}, which contains exactly one element, namely x. Many of these sets are represented using blackboard bold or bold typeface. Special sets of numbers include:
Special Sets Example:
- P or ℙ, denoting the set of all primes: P = {2, 3, 5, 7, ...}.
- N or ℕ, denoting the set of all natural numbers: N = {1, 2, 3, . . .} (sometimes defined containing 0).
- Z or ℤ, denoting the set of all integers Z = {..., −2, −1, 0, 1, 2, ...}.
- Q or ℚ, denoting the set of all rational numbers (that is, the set of all proper and improper fractions): Q = {a/b : a, b ∈ Z, b ≠ 0}.
- R or ℝ, denoting the set of all real numbers. This set includes all rational numbers, together with all irrational numbers (that is, numbers that cannot be rewritten as fractions, such as √2, as well as transcendental numbers such as π,e and numbers that cannot be defined).
- C or ℂ, denoting the set of all complex numbers : C = {a + bi : a, b ∈ R}. For example, 1 + 2i ∈ C.
- H or ℍ, denoting the set of all quaternions: H = {a + bi + cj + dk : a, b, c, d ∈ R}. For example, 1 + i + 2j − k ∈ H.
Basic Set Operations Union, Intersection, Complements, Cartesian Products
There are several fundamental operations for constructing new sets from given sets.
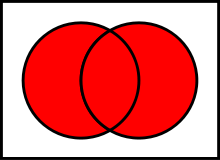
Unions:Two sets can be "added" together. The union of A and B, denoted by A ∪ B, is the set of all things that are members of either A or B.
Examples:
-
- {1, 2} ∪ {1, 2} = {1, 2}.
- {1, 2} ∪ {2, 3} = {1, 2, 3}.
Some basic properties of unions:
-
- A ∪ B = B ∪ A.
- A ∪ (B ∪ C) = (A ∪ B) ∪ C.
- A ⊆ (A ∪ B).
- A ∪ A = A.
- A ∪ ∅ = A.
- A ⊆ B if and only if A ∪ B = B.
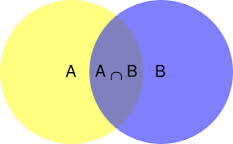
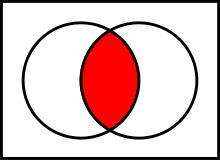
Intersections: A new set can also be constructed by determining which members two sets have "in common". The intersection of A and B, denoted by A ∩ B, is the set of all things that are members of both A and B. If A ∩ B = ∅, then A and B are said to be disjoint.
Examples:
-
- {1, 2} ∩ {1, 2} = {1, 2}.
- {1, 2} ∩ {2, 3} = {2}.
Some basic properties of intersections:
-
- A ∩ B = B ∩ A.
- A ∩ (B ∩ C) = (A ∩ B) ∩ C.
- A ∩ B ⊆ A.
- A ∩ A = A.
- A ∩ ∅ = ∅.
- A ⊆ B if and only if A ∩ B = A.
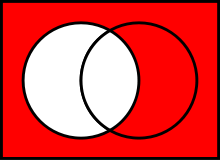
Complements: Two sets can also be "subtracted". The relative complement of B in A (also called the set-theoretic difference of A and B), denoted by A \ B (or A − B), is the set of all elements that are members of A but not members of B. Note that it is valid to "subtract" members of a set that are not in the set, such as removing the element green from the set {1, 2, 3}; doing so has no effect. In certain settings all sets under discussion are considered to be subsets of a given universal set U. In such cases, U \ A is called the absolute complement or simply complement of A, and is denoted by A′.
Examples:
-
- {1, 2} \ {1, 2} = ∅.
- {1, 2, 3, 4} \ {1, 3} = {2, 4}.
- If U is the set of integers, E is the set of even integers, and O is the set of odd integers, then U \ E = E′ = O.
Some basic properties of complements:
-
- A \ B ≠ B \ A for A ≠ B.
- A ∪ A′ = U.
- A ∩ A′ = ∅.
- (A′)′ = A.
- A \ A = ∅.
- U′ = ∅ and ∅′ = U.
- A \ B = A ∩ B′.
Cartesian Product: A new set can be constructed by associating every element of one set with every element of another set. The Cartesian product of two sets A and B, denoted by A × B is the set of all ordered pairs (a, b) such that a is a member of A and b is a member of B.
Examples:
-
- {1, 2} × {red, white} = {(1, red), (1, white), (2, red), (2, white)}.
- {1, 2} × {red, white, green} = {(1, red), (1, white), (1, green), (2, red), (2, white), (2, green) }.
- {1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.
Some basic properties of cartesian products:
-
- A × ∅ = ∅.
- A × (B ∪ C) = (A × B) ∪ (A × C).
- (A ∪ B) × C = (A × C) ∪ (B × C).
Basic Sets Example:
Fig 1: Union of set A and B denoted A ∪ B
Fig 2: Intersection of set A and B denoted A ∩ B
Fig 3: Relative Complement of set A and B
Fig 4: The complement of A in U
Basic Set Theory, Part 3
Mike BlackBasic Set Theory Part 3 - Set Operations, Complements and Subsets
Download PDFCartesian Product
randerson112358The Cartesian product A × B is the set of all ordered pairs (a, b) where a ∈ A and b ∈ B. Cartesian product is a mathematical operation that returns a set (or product set or simply product) from multiple sets.
Download PDFApplication of Sets Tables from a database
Tables and DatabasesA table is a collection of related data held in a structured format within a database. It consists of fields (columns), and rows. In relational databases and flat file databases, a table is a set of data elements (values) using a model of vertical columns (which are identified by their name) and horizontal rows, the cell being the unit where a row and column intersect. - Wikipedia
A database is a collection of information that is organized so that it can easily be accessed, managed, and updated. In one view, databases can be classified according to types of content: bibliographic, full-text, numeric, and images.
Database management systems (DBMS) are computer software applications that interact with the user, other applications, and the database itself to capture and analyze data. A general-purpose DBMS is designed to allow the definition, creation, querying, update, and administration of databases. Well-known DBMSs include MySQL, PostgreSQL, Microsoft SQL Server, Oracle, Sybase and IBM DB2.
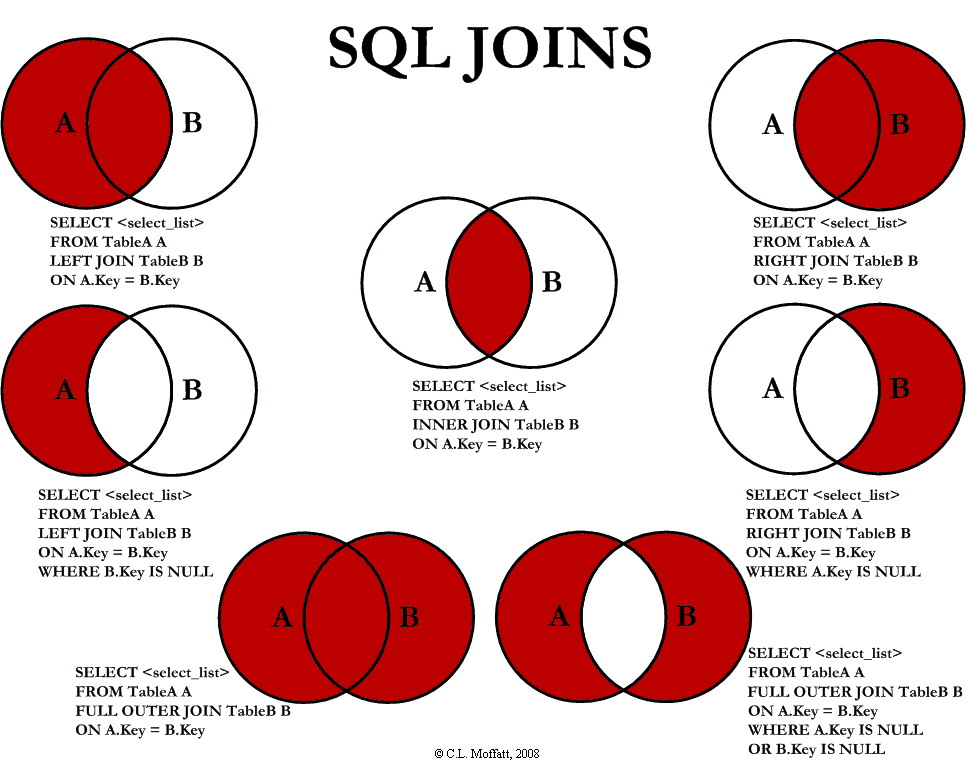
The picture to the right uses SQL to relate the tables through joins. SQL stands for Structure Query Language it is a special-purpose programming language designed for managing data held in a relational database management system, or for stream processing in a relational data stream management system.
Download PDF
SQL Statements Using NBA Data
compsci112358A set is nothing more than an unordered collection of elements with absolutely no duplicates. Formally a database refers to a set of related data and the way it is organized. Here is a video to show how you can query a database using NBA data.
Download PDFCode:
/* Created By: Rodney Anderson (randerson112358) This is an ORACLE Relational Database Query to retrieve information from tables */ SELECT name, age, TB.occupation FROM Table_A TA, Table_B TB WHERE TA.occupation = TB.key ORDER BY name DESC;