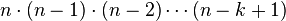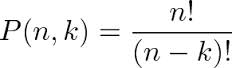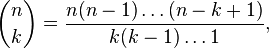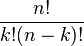Discrete Mathematics
Counting
Counting is the action of finding the number of elements of a finite set of objects.
Overview:
Counting seems easy enough: 1, 2, 3, 4, etc. This direct approach works well for counting simple things- like your toes-and may be the only approach for extremely complicated things with no identifiable structure. However, subtler methods can help you count many things in the vast middle ground, such as:
- The number of different ways to select a dozen doughnuts when there are five varieties available.
- The number of 16-bit numbers with exactly 4 ones
Perhaps surprisingly, but not coincidentally, these two numbers are the same: 1820
Combinatorics is the study of arrangements of objects, it is an important part of discrete mathematics. We must count objects to solve many different types of problems, like the determining whether there are enough telephone numbers or internet protocal (IP) addresses to meet demand. Counting techniques are also used when probabilities of events are computed.
Elementary Counting (Combinatorics)
randerson112358Solve: Given a set A, where A = {1,2,3,4,5}. How many 3 element subsets does the set A have?
Download PDFExample:
Solve: How many 3 character combinations can be made using letters AND numbers?
Answer: Their are 10 numbers in the number system ranging from (0 to 9) and their are 26 letters in the alphabet ranging from (A to Z), and their are 3 possible spots to place each character or number
This means the total number of symbols we can use in a single spot is 10 (the total possible numbers) + 26 (the total possible letters) = 36 symbols per spot.
We have 3 possible spots so our answer is 36 * 36 * 36 or 36^3 = 46,656.
Example:
How many different 10 digit phone numbers are possible in the world ?
We could simply count from 000-000-0000 to 999-999-9999, but there is a better way to count this.
There are 10 different spots available e.g. xxx-xxx-xxxx and we have 10 possible digits for each spot, numbers (0 - 9)
So the answer is 10*10*10*10*10*10*10*10*10*10 = 1010
Permutations - Counting Using Permutations
randerson112358Permutations - Counting Using Permutations. Basic info on permuatations and word problems using permutations are shown. For more free math videos, visit http://PatrickJMT.com
Download PDFPermutations Counting Without Replacement Order Matters
In mathematics, the notion of permutation relates to the act of permuting (rearranging) objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order. For example, there are six permutations of the set {1,2,3}, namely (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), and (3,2,1). As another example, an anagram of a word is a permutation of its letters. The study of permutations in this sense generally belongs to the field of combinatorics.
The number of permutations of n distinct objects is "n factorial" usually written as "n!", which means the product of all positive integers less than or equal to n.
Permutations occur, in more or less prominent ways, in almost every area of mathematics. They often arise when different orderings on certain finite sets are considered, possibly only because one wants to ignore such orderings and needs to know how many configurations are thus identified. For similar reasons permutations arise in the study of sorting algorithms in computer science.
Combinations Counting Without Replacement Order Doesn't Matter
In mathematics, a combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. If the set has n elements the number of k-combinations is equal to the binomial coefficient.
Combinations - Counting Techniques Advanced
How many words can be formed by ordering the letters ARKANSAS? randerson112358
Permutation - Counting Techniques
How many words can be formed by ordering the letters FLORIDA. randerson112358
Code:
/******************************************************************************
* Compilation: javac Combinations.java
* Execution: java Combinations N
*
* Enumerates all subsets of N elements using recursion.
* Uses some String library functions.
*
* Both functions (comb1 and comb2) print them in alphabetical
* order; comb2 does not include the empty subset.
*
* % java Combinations 3
*
* a
* ab
* abc
* ac
* b
* bc
* c
*
* a
* ab
* abc
* ac
* b
* bc
* c
*
* Remark: this is, perhaps, easier by counting from 0 to 2^N - 1 by 1
* and looking at the bit representation of the counter. However, this
* recursive approach generalizes easily, e.g., if you want to print
* out all combinations of size k.
*
******************************************************************************/
public class Combinations {
// print all subsets of the characters in s
public static void comb1(String s) { comb1("", s); }
// print all subsets of the remaining elements, with given prefix
private static void comb1(String prefix, String s) {
if (s.length() > 0) {
StdOut.println(prefix + s.charAt(0));
comb1(prefix + s.charAt(0), s.substring(1));
comb1(prefix, s.substring(1));
}
}
// alternate implementation
public static void comb2(String s) { comb2("", s); }
private static void comb2(String prefix, String s) {
StdOut.println(prefix);
for (int i = 0; i < s.length(); i++)
comb2(prefix + s.charAt(i), s.substring(i + 1));
}
// read in N from command line, and print all subsets among N elements
public static void main(String[] args) {
int N = Integer.parseInt(args[0]);
String alphabet = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ";
String elements = alphabet.substring(0, N);
// using first implementation
comb1(elements);
StdOut.println();
// using second implementation
comb2(elements);
StdOut.println();
}
}