Discrete Mathematics
Recurrence Relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms.
Overview:
Recurrence relations are used to determine the running time
of recursive programs – recurrence relations themselves are
recursive.
T(0) = Time to solve problem of size 0
T(n) = Time to solve problem of size n
There are many ways to solve a recurrence relation running time:
1) Back substitution
2) By Induction
3) Use Masters Theorem
4) Recursion tree
Examples of recurrence relations:
- T( n ) = T(n -1) + 1, T( 0 ) = 1
- F( n ) = F(n -1) + F(n-2) , F(1) =1 , F(0) = 1 Fibbanocci Sequence
- an = an-1 + 3 , a0=5
- 5, 8, 11, 14, 17, 20, 23, ...
Solve recurrence Relation By Iterative Substitution
randerson112358This is a tutorial on solving a recurrence relation using the iterative substitution method.
Download PDFSolve Recurrence Relation Proof by iteration
Solve Recurrence Relation Masters Theorem
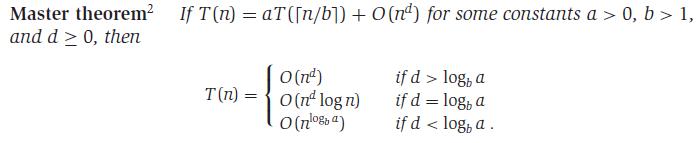
Example: T(n) = 4T(n/2) + n
Reading from the equation, a = 4, b=2, f(n) = n1, so d = 1.
d < logba = 1 < log24
so n = O( nlog24) = O( n2 )
Site PDF
Solve recurrence relation by Master Theorem
randerson112358Solve recurrence relation using Master Theorem
SiteCode: T(n)= T(n-1) +3, T(0) = 5
/*
C Program for simple recursion
This program similates the recurrence relation function , T(n) = T(n-1) +3, T(0)=5.
By: randerson112358
*/
# include < stdio.h >
int T( int n); // Defining function T().
int main(void)
{
int n = 8;
int i;
for(i=0; i < n; i++)
{
printf("T(%d) = %d\n", i, T(i) ); // prints 5, 8, 11, 14, 17, 20, 23, 26
}
//Comment out the system("pause") if you are not using Windows
system("pause");
}
int T( int n)
{
if( n == 0)
return 5;
else
return T(n-1) + 3;
}