Discrete Mathematics
Stacks and Queues
Stack is a container of objects that are inserted and removed according to the last-in first-out (LIFO) principle.
Queue is a container of objects (a linear collection) that are inserted and removed according to the first-in first-out (FIFO) principle.
Overview
Stack:
In the pushdown stacks only two operations are allowed: push the item into the stack, and pop the item out of the stack. A stack is a limited access data structure - elements can be added and removed from the stack only at the top. push adds an item to the top of the stack, pop removes the item from the top. A helpful analogy is to think of a stack of books; you can remove only the top book, also you can add a new book on the top.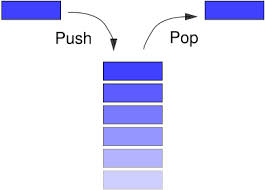
Queue:
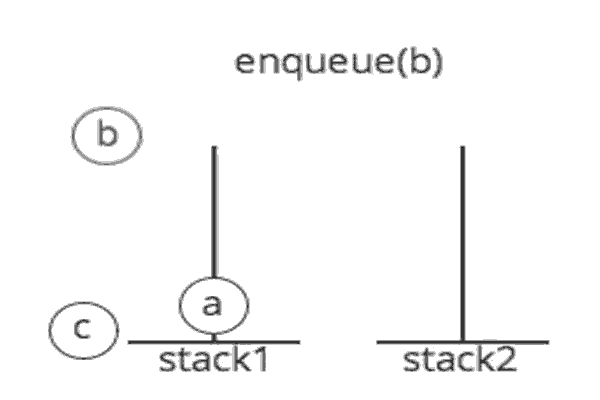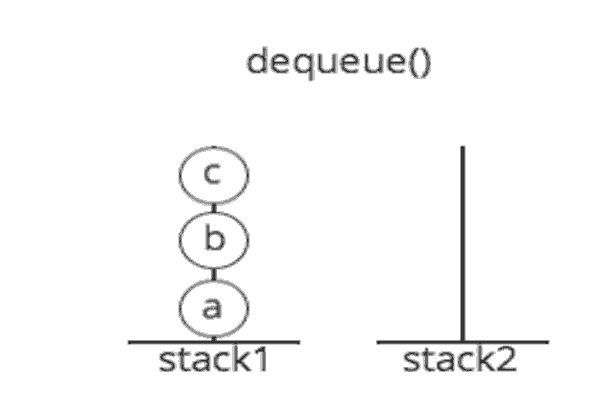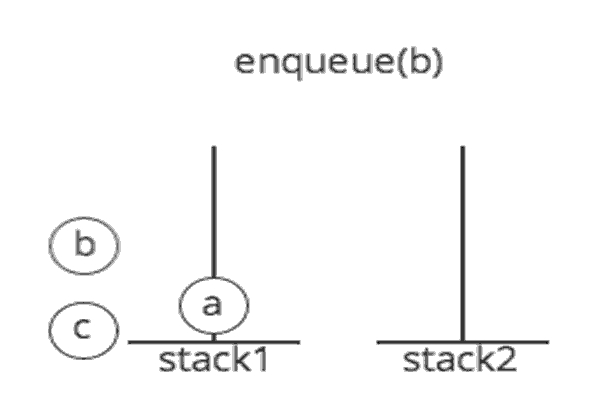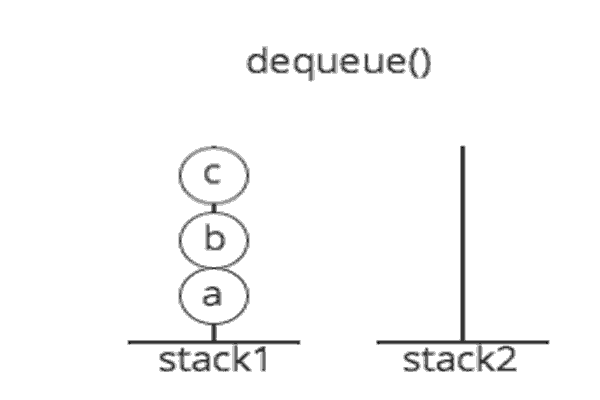
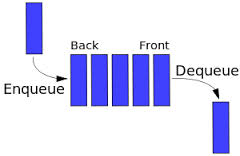
An excellent example of a queue is a line of students in the food court of the UC. New additions to a line made to the back of the queue, while removal (or serving) happens in the front. In the queue only two operations are allowed enqueue and dequeue. Enqueue means to insert an item into the back of the queue, dequeue means removing the front item. The picture demonstrates the FIFO access.
The difference between stacks and queues is in removing. In a stack we remove the item the most recently added; in a queue, we remove the item the least recently added.
FIFO & LILO and LIFO & FILO Principles
Queue: First In First Out (FIFO): The first object into a queue is the first object to leave the queue, used by a queue.
Stack: Last In First Out (LIFO): The last object into a stack is the first object to leave the stack, used by a stack
OR
Stack: First In Last Out (FILO): The first object or item in a stack is the last object or item to leave the stack.
Queue: Last In Last Out (LILO): The last object or item in a queue is the last object or item to leave the queue.
Easy Stacks and Queues
randerson112358Easy and simple explaination on stacks and queues
Download PDFStack C Code:
// Arup Guha
// 6/20/07
// Written in COP 3502 to illustrate an array implementation of a stack.
#include <stdio.h>
// The array will store the items in the stack, first in
// index 0, then 1, etc. top will represent the index
// to the top element in the stack. If the stack is
// empty top will be -1.
#define SIZE 10
#define EMPTY -1
struct stack {
int items[SIZE];
int top;
};
void initialize(struct stack* stackPtr);
int full(struct stack* stackPtr);
int push(struct stack* stackPtr, int value);
int empty(struct stack* stackPtr);
int pop(struct stack* stackPtr);
int top(struct stack* stackPtr);
int main() {
int i;
struct stack mine;
// Set up the stack and push a couple items, then pop one.
initialize(&mine);
push(&mine, 4);
push(&mine, 5);
printf("Popping %d\n", pop(&mine));
// Push a couple more and test top.
push(&mine, 22);
push(&mine, 16);
printf("At top now = %d\n", top(&mine));
// Pop all three off.
printf("Popping %d\n", pop(&mine));
printf("Popping %d\n", pop(&mine));
printf("Popping %d\n", pop(&mine));
// Checking the empty function.
if (empty(&mine))
printf("The stack is empty as expected.\n");
// Fill the stack.
for (i = 0; i<10; i++)
push(&mine, i);
// Check if full works.
if (full(&mine))
printf("This stack is full as expected.\n");
// Pop everything back off.
for (i = 0; i<10; i++)
printf("popping %d\n",pop(&mine));
system("PAUSE");
return 0;
}
void initialize(struct stack* stackPtr) {
stackPtr->top = -1;
}
// If the push occurs, 1 is returned. If the
// stack is full and the push can't be done, 0 is
// returned.
int push(struct stack* stackPtr, int value) {
// Check if the stack is full.
if (full(stackPtr))
return 0;
// Add value to the top of the stack and adjust the value of the top.
stackPtr->items[stackPtr->top+1] = value;
(stackPtr->top)++;
return 1;
}
// Returns true iff the stack pointed to by stackPtr is full.
int full(struct stack* stackPtr) {
return (stackPtr->top == SIZE - 1);
}
// Returns true iff the stack pointed to by stackPtr is empty.
int empty(struct stack* stackPtr) {
return (stackPtr->top == -1);
}
// Pre-condition: The stack pointed to by stackPtr is NOT empty.
// Post-condition: The value on the top of the stack is popped and returned.
// Note: If the stack pointed to by stackPtr is empty, -1 is returned.
int pop(struct stack* stackPtr) {
int retval;
// Check the case that the stack is empty.
if (empty(stackPtr))
return EMPTY;
// Retrieve the item from the top of the stack, adjust the top and return
// the item.
retval = stackPtr->items[stackPtr->top];
(stackPtr->top)--;
return retval;
}
// Pre-condition: The stack pointed to by stackPtr is NOT empty.
// Post-condition: The value on the top of the stack is returned.
// Note: If the stack pointed to by stackPtr is empty, -1 is returned.
int top(struct stack* stackPtr) {
// Take care of the empty case.
if (empty(stackPtr))
return EMPTY;
// Return the desired item.
return stackPtr->items[stackPtr->top];
}
Queue C Code:
// Arup Guha
// 6/26/07
// Example of how to implement a queue with an array.
#include <stdio.h>
#define EMPTY -1
#define INIT_SIZE 10
// Stores our queue.
struct queue {
int* elements;
int front;
int numElements;
int queueSize;
};
void init(struct queue* qPtr);
int enqueue(struct queue* qPtr, int val);
int dequeue(struct queue* qPtr);
int empty(struct queue* qPtr);
int front(struct queue* qPtr);
int main() {
int i;
// Allocate space for our queue and initialize it.
struct queue* MyQueuePtr = (struct queue*)malloc(sizeof(struct queue));
init(MyQueuePtr);
// Enqueue some items.
enqueue(MyQueuePtr, 3);
enqueue(MyQueuePtr, 7);
enqueue(MyQueuePtr, 4);
// Try one dequeue.
printf("Dequeue %d\n", dequeue(MyQueuePtr));
// Enqueue one more item, then try several dequeues and one front.
enqueue(MyQueuePtr, 2);
printf("Dequeue %d\n", dequeue(MyQueuePtr));
printf("At Front of Queue Now: %d\n", front(MyQueuePtr));
printf("Dequeue %d\n", dequeue(MyQueuePtr));
printf("Dequeue %d\n", dequeue(MyQueuePtr));
// See if we can detect an empty queue.
printf("Is empty: %d\n", empty(MyQueuePtr));
// Try enqueuing and dequeuing again to make sure that our previous
// operations didn't "corrupt" the queue.
enqueue(MyQueuePtr, 5);
enqueue(MyQueuePtr, 9);
// Try lots of enqueues to test the dynamic capability of the queue.
for (i=30; i<60; i++)
enqueue(MyQueuePtr, i);
// Dequeue everything.
while (!empty(MyQueuePtr))
printf("Dequeue %d\n", dequeue(MyQueuePtr));
return 0;
}
// Pre-condition: qPtr points to a valid struct queue.
// Post-condition: The struct that qPtr points to will be set up to represent an
// empty queue.
void init(struct queue* qPtr) {
// The front index is 0, as is the number of elements.
qPtr->elements = (int*)malloc(sizeof(int)*INIT_SIZE);
qPtr->front = 0;
qPtr->numElements = 0;
qPtr->queueSize = INIT_SIZE;
}
// Pre-condition: qPtr points to a valid struct queue and val is the value to
// enqueue into the queue pointed to by qPtr.
// Post-condition: If the operation is successful, 1 will be returned, otherwise
// no change will be made to the queue and 0 will be returned.
// Note: Right now, I don't know how to detect that the realloc failed, so 0
// does not get returned.
int enqueue(struct queue* qPtr, int val) {
int i;
// Regular case where our queue isn't full.
if (qPtr->numElements != qPtr->queueSize) {
// Enqueue the current element. Note the use of mod for the wraparound
// case. Edit the number of elements.
qPtr->elements[(qPtr->front+qPtr->numElements)%qPtr->queueSize] = val;
(qPtr->numElements)++;
// Signifies a successful operation.
return 1;
}
// Case where the queue is full, we must find more space before we enqueue.
else {
// Allocate more space!
qPtr->elements = realloc(qPtr->elements, (qPtr->queueSize)*sizeof(int)*2);
// Copy all of the items that are stored "before" front and copy them
// into their new correct locations.
for (i=0; i<=qPtr->front-1; i++)
qPtr->elements[i+qPtr->queueSize] = qPtr->elements[i];
// Enqueue the new item, now that there is space. We are guaranteed that
// no wraparound is necessary here.
qPtr->elements[i+qPtr->queueSize] = val;
// More bookkeeping: The size of the queue as doubled and the number of
// elements has increased by one.
(qPtr->queueSize) *= 2;
(qPtr->numElements)++;
return 1;
}
}
// Pre-condition: qPtr points to a valid struct queue.
// Post-condition: If the queue pointed to by qPtr is non-empty, then the value
// at the front of the queue is deleted from the queue and
// returned. Otherwise, -1 is returned to signify that the queue
// was already empty when the dequeue was attempted.
int dequeue(struct queue* qPtr) {
int retval;
// Empty case.
if (qPtr->numElements == 0)
return EMPTY;
// Store the value that should be returned.
retval = qPtr->elements[qPtr->front];
// Adjust the index to the front of the queue accordingly.
qPtr->front = (qPtr->front + 1)% qPtr->queueSize;
// We have one fewer element in the queue.
(qPtr->numElements)--;
// Return the dequeued element.
return retval;
}
// Pre-condition: qPtr points to a valid struct queue.
// Post-condition: returns true iff the queue pointed to by pPtr is empty.
int empty(struct queue* qPtr) {
return qPtr->numElements == 0;
}
// Pre-condition: qPtr points to a valid struct queue.
// Post-condition: if the queue pointed to by qPtr is non-empty, the value
// stored at the front of the queue is returned. Otherwise,
// -1 is returned to signify that this queue is empty.
int front(struct queue* qPtr) {
if (qPtr->numElements != 0)
return qPtr->elements[qPtr->front];
else
return EMPTY;
}